4G/LTE - PHY Channel

PBCH (Physical Broadcast Channel)

PBCH is a special channel to carry MIB and has following characteristics :

It carries only the MIB.
It is using QPSK.
Mapped to 6 Resource Blocks (72 subcarriers), centered around DC subcarrier in sub frame 0.
Mapped to Resource Elements which is not reserved for transmission of reference signals, PDCCH or PHICH

Followings are the topics that will be described in this page.

BCH Physical Layer Processing

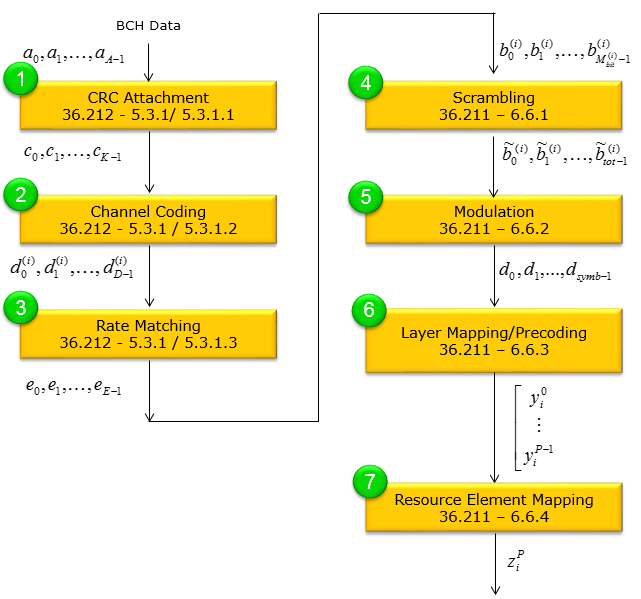
BCH Physical Layer Processing

In terms of data processing, it goes through the following steps. If you are seriously intersted in physical layer channel processing but PDSCH is too complicated for you to start, try following through each and every steps of PBCH processing as shown below and refer to 3GPP specification over and over whenever you have time.

Refer to Precoding page for step (6). If you are also interested more in Step (6) in terms of Antenna Configuration, Refer to PHY Processing page.

If you want to have more concrete implementation of this process, you may refer to Matlab :ToolBox : LTE : Downlink : PBCH

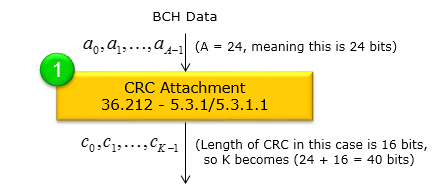
CRC Attachement : 36.212-5.3.1

This is the step where CRC(Cyclic Redundancy Check) is attached to BCH (Broadcast Channel) transport block. The brief summary of this process is :

Compute a 16-bit CRC over the 24-bit BCH transport block.
Append these 16 CRC bits, yielding 40 bits.
Scramble (XOR) only the 16 CRC bits with a known mask (x_ant,0 … x_ant,15) depending on the number of eNodeB transmit antennas.
The resulting 40 bits (c₀, …, c₃₉) form the PBCH to be transmitted.

Following is a step-by-step explanation of how the CRC is attached to the BCH transport block and then “scrambled” (masked) depending on the eNodeB’s transmit antenna configuration.

Step 1. Transport Block and CRC Size

A BCH transport block has size A = 24 bits. Denote these bits as:
a₀, a₁, a₂, …, a_A−1.
A 16-bit CRC is computed over all 24 bits, so there are L = 16 parity bits:
p₀, p₁, p₂, …, p_L−1.

Step 2. Computing the CRC

Layer 1 takes the 24 data bits (a₀, a₁, …, a₂₃).
It uses a standard CRC generator polynomial to calculate the 16 CRC bits (p₀, p₁, …, p₁₅).
These 16 bits are appended to the original 24 bits, making a total of 40 bits. Conceptually (before scrambling):
c₀, c₁, …, c₂₃, c₂₄, …, c₃₉, where
c_k = a_k for k = 0..23 and c_{24 + i} = p_i for i = 0..15.

Step 3. Scrambling (Masking) the CRC Bits

Let x_{ant, 0}, x_{ant, 1}, …, x_{ant, 15} be the known scrambling (mask) bits, which depend on the eNodeB’s transmit antenna configuration. The table provides three possible masks:
- 1 antenna port: <0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0>
- 2 antenna ports: <1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1>
- 4 antenna ports: <0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1>
The first 24 bits (a₀ … a₂₃) are unchanged:
c_k = a_k, for k = 0..23.
For the 16 CRC bits, each one is XOR-ed (mod 2) with the corresponding mask bit:
c_k = (p_k−A + x_{ant, k−A}) mod 2, for k = A..(A+15) = 24,25,..,39.
This means:
p_i → p_i ⊕ x_{ant, i} (for i = 0..15).

NOTE : A represents the size of the BCH (Broadcast Channel) transport block in bits. For the PBCH (Physical Broadcast Channel), A = 24, meaning that the transport block consists of 24 bits before the 16-bit CRC is computed and attached.

NOTE Why Scramble the CRC?

Identification of antenna configuration: The UE tries different masks (all zeros, all ones, or alternating) to find which mask yields a valid CRC. This way it knows the actual antenna configuration of the eNodeB.
Robustness: Scrambling helps ensure reliable decoding of the PBCH in various network deployments.

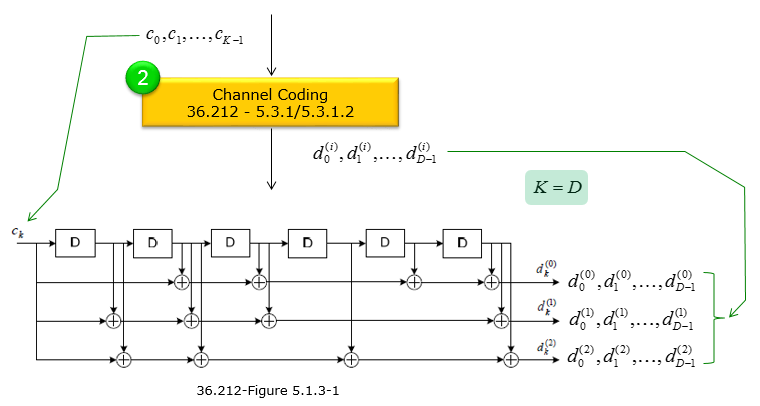
Channel Coding : 36.212-5.3.1

Channel coding adds controlled redundancy to the transmitted data so that the receiver can detect and/or correct bit errors caused by noise, interference, and other impairments on the radio channel. In short, channel coding (e.g., convolutional coding, turbo coding, LDPC, etc.) improves the reliability and robustness of wireless communication links by allowing error correction mechanisms at the receiver.

For BCH, a channel coding called 'Tail-Biting Convolutional' is used. Tail-biting convolutional coding ensures the encoder starts and ends in the same state without appending extra “tail” bits. In other words, the encoder effectively “wraps around” so that the last encoded bit transitions smoothly back to the initial state. This avoids the overhead of flushing the encoder registers, preserving throughput while still offering error correction capabilities.

The overall channel coding process for BCH can be summarized as below.

The size of array c[] is 24 (K = 24) and output of channel coding is 72 in total(each of three d[] array is 24 bits). The coding method is based on 36.212-5.1.3.1 Tail biting convolutional coding as brielfy illustrated below.

In this channel-coding procedure, the input bits c₀, c₁, …, c_K−1 are passed through a tail-biting convolutional encoder in order to generate three separate output bit streams. Each output stream has the same length as the input (K), and so you get a total of 3×K coded bits.

Below is a step-by-step outline of how the process works,.

Input Bits (c_k) The information bits entering the channel encoder are labeled c₀, c₁, c₂, …, c_K−1. Here, K is the number of bits in the input block (for example, K = 24 for the PBCH).
Tail-Biting Convolutional Encoder The tail-biting approach means the convolutional encoder’s shift registers are initialized to the final K−1 bits of the input sequence (conceptually wrapping the end of the sequence around to the beginning). By doing so, we avoid appending extra “tail bits” at the end, and ensure the encoder’s end-state matches its start-state without adding overhead.
Encoding Rate and Outputs (d⁽ⁱ⁾_k) This convolutional code is typically rate 1/3: for every single input bit c_k, the encoder produces 3 output bits, labeled d⁽⁰⁾_k, d⁽¹⁾_k, d⁽²⁾_k. Thus, each output stream d⁽ⁱ⁾ has exactly D = K bits: d⁽ⁱ⁾₀, d⁽ⁱ⁾₁, …, d⁽ⁱ⁾_K−1 for i = 0, 1, 2.
Total Output Bits Since there are three coded streams each of length K, the total number of coded bits becomes 3 × K. For example, if K = 24, then you get 3 × 24 = 72 output bits in total.
Illustration The figure (e.g., 36.212-Figure 5.1.3-1) shows a typical 6-register convolutional encoder with feedback taps. Each input bit c_k is shifted in, combined (via XOR) in different ways to produce the three outputs d⁽⁰⁾_k, d⁽¹⁾_k, d⁽²⁾_k. Tail biting means the state after processing c_K−1 “wraps around” to match the initial state before processing c₀.

Example Flow (K=24):

If you really understand the details and try manually or with your own program. Please try following example.

You have an input array c[] of 24 bits.
These bits are passed through the tail-biting convolutional encoder.
You obtain three output arrays d⁽⁰⁾[], d⁽¹⁾[], and d⁽²⁾[], each 24 bits long.
The total output is 72 bits, which can then undergo further processing (e.g., modulation, mapping to resource elements, etc.).

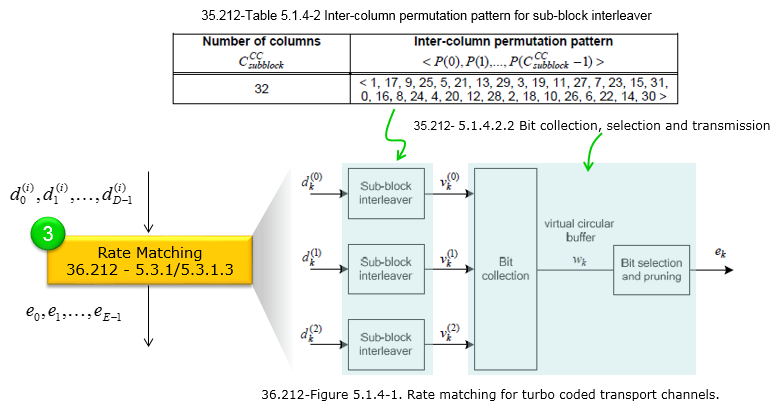
c[] = { 0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0 }

d1[] = { 0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,1,1,0,1,1,0,0,0,0 }

d2[] = { 0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,0,0,1,0,0,0,0 }

d3[] = { 0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,0,1,0,1,0,0,0,0 }

Rate Matching : 36.212-5.3.1

Rate matching selects (or sometimes repeats and punctures) coded bits in a way that produces exactly the required number of bits for transmission (E). It adjusts the effective code rate to match the available resources and target data throughput without compromising error correction performance.

After the convolutional encoder produces three coded bit streams (d⁽⁰⁾_k, d⁽¹⁾_k, d⁽²⁾_k for k = 0..D−1), these streams are delivered to the rate matching block. Rate matching ensures that the total number of transmitted bits (E) matches the required code rate or available resource space (e.g., for PBCH).

The bits d⁽ⁱ⁾₀, …, d⁽ⁱ⁾_D−1 (i = 0,1,2) are processed using the following main steps:

Sub-block Interleaving
Each coded stream (d⁽ⁱ⁾) passes through a sub-block interleaver, which rearranges (permutes) the bits based on a predefined pattern. This helps further randomize the bit sequence to improve error resilience.
Bit Collection
After sub-block interleaving, all bits are collected into a virtual circular buffer. Think of this as placing the interleaved bits into a circular arrangement so that reading can “wrap around” if necessary.
Bit Selection & Pruning
From this circular buffer, only a certain number of bits (E) are chosen (or “pruned”) according to the required rate. This pruning process ensures that the final output bit stream has exactly E bits: e₀, e₁, …, e_E−1.

This entire “rate matching” process adjusts how many coded bits are ultimately transmitted, letting the system adapt to the available channel resources or target code rate. The final output e_k (k = 0..E−1) goes on to modulation and physical-layer mapping.

In summary, rate matching takes the three streams of tail-biting convolutionally coded bits and produces a final stream of size E. By doing so, it controls the effective coding rate for the PBCH or other physical channels.

NOTE 1 :How to figure out 'D' value ?

:D is the number of bits in each of the three coded streams produced by the tail-biting convolutional encoder. Because it is “tail-biting,” no extra tail bits are added, so D = K (the input block size). For example, if K = 24 information bits go in, each of the three output streams has D = 24 bits, giving a total of 72 bits.

NOTE 2 :How to figure out 'E' value ?

E is the number of bits after rate matching. It depends on how many bits must be transmitted for that channel (determined by the standard or by the physical resource allocation). The rate matching process (e.g., puncturing, repetition, or just “bit selection”) prunes or repeats coded bits so that the final output has exactly E bits. Figuring out E value is a challenge because it would vary depending on situation but for LTE PBCH case it is a fixed value since the number of physical resources (Resource Elements) and modulation scheme is fixed. Followings are further details,

For the normal CP case in LTE, the PBCH is rate-matched to E = 240 bits per 10 ms radio frame. These 240 bits are then re-transmitted (or “repeated”) repeated over four consecutive radio frames (a 40 ms period), but each repetition still corresponds to the same 240-bit codeword.

Why 240 Bits? Below is a simplified way to see where “240” comes from for normal CP and a single antenna port.

Resource Elements for PBCH The PBCH occupies the central 6 RBs (i.e., 72 subcarriers) over 4 OFDM symbols in subframe 0. Total REs in that region: 72 × 4 = 288.
Reference Signal Overhead Even with one transmit antenna, a small number of those 288 REs are used by the cell-specific reference signal (CRS). After subtracting these overhead REs, the remaining REs are available for PBCH data. (If more antenna ports are used, overhead increases, but the standard still defines the final PBCH block size to be 240 bits for normal CP.)
QPSK Modulation = 2 bits/RE Each “data-carrying” resource element with QPSK conveys 2 bits. The exact count ends up yielding a net 240 data bits after the reference signals are accounted for. In other words, you can think of the total bits (288 RE × 2) minus overhead, with standard rounding and definitions, giving you 240 bits for the PBCH codeword.
Rate Matching to 240 Bits After convolutional encoding (3 × K bits) and sub-block interleaving, the rate matching block “selects” exactly E = 240 bits to transmit for the PBCH in each 10 ms frame (that is, each radio frame).

Hence, E = 240 is fixed by the PBCH’s resource mapping and overhead design for normal CP. For extended CP, it is slightly different (typically E = 224 bits).

NOTE 3 :How subblock interleaver works ?

A sub-block interleaver rearranges coded bits in two steps:

Loading the Matrix – a bit sequence are written row by row into a matrix with a fixed number of columns (for example, 32). The number of rows depends on how many bits need to be interleaved.
Reading Out with a Permutation – Instead of reading columns sequentially, it follows a predefined permutation pattern (like a shuffled order of the column indices). This spreads the bits more evenly and helps protect against burst errors because bits originally close to each other end up being spaced apart after interleaving.
Serializing back : After you finish reading the columns in the permuted order, all of the bits are concatenated (serialized) into a single output bitstream, effectively re-forming a continuous sequence (but in a new, interleaved order).

At the second step (i.e, reading out with a permutation) the Table 5.1.4-2 plays the crucial role. The bit sequence are first placed into a matrix having a certain number of columns (e.g., 32). Once the bits are loaded into this matrix row by row, the columns are read out in a permuted order according to the sequence provided in Table 5.1.4-2.

Below is a brief overview of the meaning behind this table:

Number of Columns
The table specifies how many columns are used for the interleaver (e.g., 32). This determines the width of the matrix in which the bits are arranged.
Permutation Pattern <P(0), P(1), …, P(C−1)>
This shows the exact order in which the columns should be read out (or “permuted”). For example, instead of reading columns 0, 1, 2, 3, …, the table might say <1, 17, 9, 25, 5, …> and so on. That means you read column 1 first, then column 17, then column 9, etc., until all columns have been read.
Purpose of Column Permutation
By rearranging the columns in a non-sequential order, the bits become more “randomized” when placed back into the bitstream. This helps to spread out burst errors and boost error correction performance, since correlated errors are less likely to occur in adjacent bits of the final output sequence.

In other words, Table 5.1.4-2 defines the column “shuffling” pattern that the sub-block interleaver applies to improve the robustness and efficiency of the coding process.

NOTE 4 :How bit selection works ?

Bit collection is essentially the final step of rate matching where the circular buffer is read (with a possible offset k₀) until exactly E bits are gathered. Any NULL bits are skipped. This process shapes how the final coded bits are transmitted, enabling different redundancy versions and ensuring the desired code rate is achieved.

In short This procedure ensures different redundancy versions pick different parts of the circular buffer for incremental redundancy or puncturing, thereby optimizing HARQ performance and code-rate flexibility.

Following is overall procedure of the bit selection process.

You create the circular buffer w of length K_w = 3 × K_Π by combining the systematic and parity streams (v⁽⁰⁾, v⁽¹⁾, v⁽²⁾).
You compute N_cb, which may cap how many bits are actually usable in w (the rest can be NULL).
You figure out E, the number of bits needed from w for this code block, based on the total bits G for the transport block, the number of code blocks C, and the modulation/layering parameters.
You read from w starting at offset k₀ (determined by rv_idx), skipping any NULL entries, until you have gathered exactly E bits. These bits become e₀, …, e_E−1, the final rate-matched output for that code block.

Followings are breakdown of the bit selection process based on 36.212-5.1.4.1.2

In the LTE rate-matching procedure, bit collection describes how the convolutionally or turbo-coded bits (already interleaved) are placed into (and then read from) a circular buffer to form the final stream of E bits for transmission.

Step 1. Forming the Circular Buffer (w)

Three Coded Streams : After sub-block interleaving, you have three separate streams of coded bits: v⁽⁰⁾, v⁽¹⁾, v⁽²⁾, each of length K_Π. These correspond to systematic bits v⁽⁰⁾ and two sets of parity bits v⁽¹⁾, v⁽²⁾.
Circular Buffer Size : Define K_w = 3 × K_Π. This is the total size of the circular buffer.
Loading Bits into w : You place v⁽⁰⁾ (systematic bits) in the first K_Π positions of w. Then you interleave the parity bits for the next 2K_Π positions:
- w_k = v⁽⁰⁾_k for k = 0..K_Π−1
- w_{K_Π + 2k} = v⁽¹⁾_k
- w_{K_Π + 2k + 1} = v⁽²⁾_k
This forms a single circular buffer w containing all systematic and parity bits.

Step 2. Determining N_cb

Soft Buffer Partitioning If this is for a DL-SCH (downlink), the specification defines a soft buffer size N_IR. If you split the transport block into C code blocks, each code block gets: N_cb = min( floor(N_IR/C), K_w ).
UL-SCH and MCH Cases For uplink or MCH, N_cb = K_w (no truncation).
Purpose N_cb caps how many bits are used from the circular buffer for that code block. If N_cb < K_w, some entries in w become NULL.

Step 3. Computing E (Rate-Matched Output Bits)

Total Bits G for the Transport Block G is the total number of bits to be transmitted for the transport block after taking into account the modulation scheme and layer mapping. Let G' = G / (N_L × Q_m), where:
- Q_m is the modulation order (2 for QPSK, 4 for 16QAM, 6 for 64QAM).
- N_L is the number of layers.
We divide G' among the C code blocks.
Final E for the r-th Code Block Depending on r and γ = G' mod C, some code blocks get N_L × Q_m × floor(G'/C) bits, and others get N_L × Q_m × ceil(G'/C). The result is E, the number of output bits for that code block.

Step 4. Picking Bits from w (Bit Collection)

Offset k₀ The specification calculates an offset k₀ based on redundancy version (rv_idx) and the sub-block size, ensuring different redundancy versions pick bits from different starting points in the circular buffer.
Selecting E Bits We set k = 0 and j = 0. While k < E:
- Candidate bit = w_{(k₀ + j) mod N_cb}.
- If that candidate is not NULL, it becomes e_k and we increment k.
- We always increment j regardless.
We stop once we have collected exactly E non-NULL bits, forming e₀, e₁, …, e_E−1.

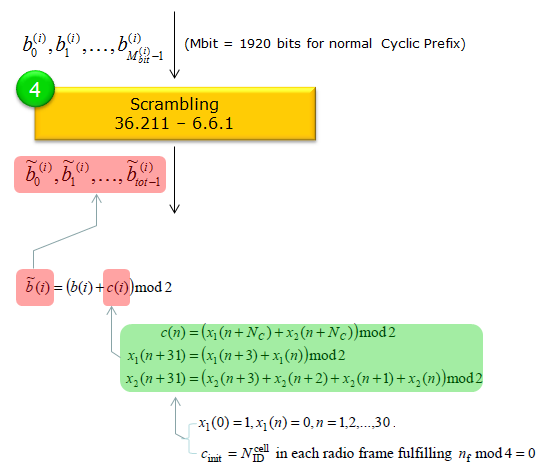
Scrambling : 36.211-6.6.1

Scrambling randomizes the transmitted bits and helps mitigate interference from other cells using different scrambling codes. It also aids in reducing undesirable signal characteristics (like high peak-to-average power).

Scrambling in LTE PBCH is essentially a bitwise XOR process that uses a cell-specific pseudorandom sequence. It randomizes the transmitted bits to help mitigate interference and reduce undesired signal characteristics such as high peak-to-average power. Each cell’s unique scrambling sequence is initialized using its cell ID, ensuring that overlapping cells do not interfere as severely. The output bit length remains the same, but each bit is toggled according to the scrambling pattern prior to modulation. This ensures that each cell’s PBCH has a unique scrambling pattern, improving cell-specific detection and overall system performance.

Following is the overall procedure of the scrambling process

Start with M_bit PBCH bits b(i).
Generate the scrambling sequence c(i) based on c_init = N_ID^cell.
Perform a bitwise XOR: b(i) = b(i) + c(i) mod 2.
Modulate and map these scrambled bits onto the PBCH resources.

The image above shows how the PBCH bits are scrambled using a cell-specific sequence. This process applies to the M_bit bits of the PBCH: 1920 bits for normal cyclic prefix or 1728 bits for extended cyclic prefix.

Following is the break down of the detailed process

Step 1. Input Bits b(i)

Before scrambling, you have a block of bits: b(0), b(1), …, b(M_bit – 1), where M_bit is either 1920 or 1728 depending on the cyclic prefix. These bits have already passed through the channel coding and rate matching steps.

Step 2. Scrambling Sequence c(i)

Each bit b(i) is XOR-ed (mod 2) with the cell-specific scrambling sequence c(i): b(i) = b(i) + c(i) mod 2.
The sequence c(i) is defined in 3GPP TS 36.211 - 7.2. It uses two pseudo-random sequences x₁(n) and x₂(n) with well-defined generator polynomials.
The initialization parameter c_init = N_ID^cell ensures that each cell scrambles the PBCH differently, so UEs can distinguish between cells.

Step 3. Output Bits b(i)

The result of scrambling is a new sequence of bits ~b(0), ~b(1), …, ~b(M_bit – 1).. The number of bits remains the same as before ( 1920 or 1728). These scrambled bits then undergo modulation (e.g., QPSK) and are mapped onto the PBCH resource elements.

NOTE :Why the size of the input is 1920 bits ?

If you were following the process carefully, you may find some strange thing at this point. The output bit length of rate matching (the prior step) is 240 bits. Usually the output of a prior step(rate matching in this case) become the input of the next step (scrambling in this case). Why there is the discrepancies in terms of the bit length between the output of rate matching and the input of scrambling ?

The short answer is that the specification counts the total bits over the four repeated PBCH transmissions (each 240-bit codeword is mapped and repeated) and accounts for 2 bits per resource element with QPSK. Although the rate matching step produces 240 bits for a single codeword, the next stage (scrambling) sees the entire four-transmission set (240 × 4 = 960) along with the 2 bits/RE detail, resulting in 1920 bits being scrambled in total.

Followings are the detailed breakdown of the answer

Single Subframe (10 ms Frame) Mapping

In each 10 ms radio frame, the PBCH occupies 4 OFDM symbols in subframe #0 (not four separate transmissions in that subframe). For normal CP and a single antenna port, there are 72 subcarriers × 4 symbols = 288 resource elements (REs) total for the PBCH region. After accounting for reference signals, you end up with 240 useful bits per subframe to carry the PBCH codeword.

Four Consecutive Frames (40 ms) Repetition

The same 240-bit PBCH codeword is transmitted again in subframe #0 of the next 3 frames. That’s a total of 4 identical transmissions in frames #0, #1, #2, and #3 (spanning 40 ms). This repetition (one per 10 ms frame) is what gives a UE multiple chances to decode the broadcast information.

Why 1920 Bits in the Specification?

After rate matching, you have a 240-bit codeword for a single PBCH transmission in one subframe. However, from the perspective of the scrambler and QPSK modulation across a full 40 ms repetition period, standards often talk about M_bit = 1920 bits. That comes from 240 bits × 2 (QPSK) × 4 transmissions, or from the view that you have 960 REs × 2 bits each. The exact wording in the spec can sometimes make it seem like 1920 bits are used “at once,” but it’s effectively counting the total bits that appear over the four repeated transmissions.

Bottom Line

One codeword = 240 bits (for normal CP, single antenna port).
Mapped to subframe #0 of one 10 ms frame (occupies 4 OFDM symbols there).
Repeated in subframe #0 of 3 subsequent frames → 4 total transmissions (40 ms).
1920 bits in the spec typically refers to the total bits over those four transmissions and the 2 bits/RE of QPSK.

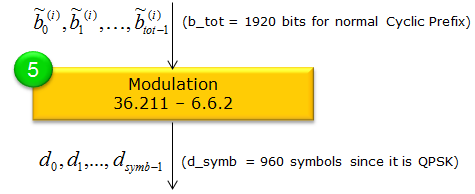
Modulation : 36.211-6.6.2

After the PBCH bits have been scrambled, the resulting sequence ~b(0), ~b(1), …, ~b(M_bit−1) is mapped to complex-valued symbols using QPSK, as specified in the specification.

In QPSK, every pair of bits forms one modulation symbol. That means if M_bit is the total number of scrambled bits, the number of symbols, M_symb, becomes M_bit / 2.

For the PBCH, QPSK is always used. Hence:

Normal CP: M_bit = 1920 → M_symb = 1920 / 2 = 960 symbols
Extended CP: M_bit = 1728 → M_symb = 1728 / 2 = 864 symbols

Each complex QPSK symbol (e.g., d(0), d(1), …, d(M_symb−1)) is placed onto the PBCH resource elements in subframe 0 for transmission over the air. This final modulation step transforms the scrambled bits into waveforms suitable for the physical downlink channel.

Resource Element Mapping : 36.211-6.6.4

Resource element mapping refers to the process of placing the modulated symbols onto specific subcarrier and OFDM symbol positions in the LTE time-frequency grid. It ensures each bit of data is transmitted in a known, standardized location, taking into account the resource elements reserved for reference signals or other overhead. By defining a clear mapping sequence, the system guarantees that both the transmitter and receiver align on where data and control information should be sent and received

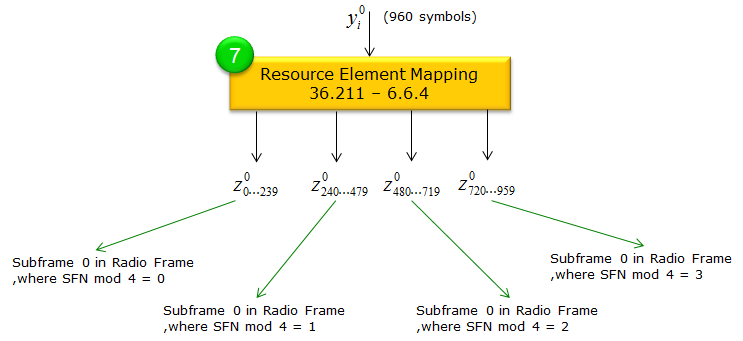
After QPSK modulation, we have M_symb complex symbols {y^(p)(0), …, y^(p)(M_symb−1)} for antenna port p. In the normal CP case, M_symb = 960 (i.e., 240 bits × 2 bits/symbol × 4 transmissions). These symbols are transmitted during 4 consecutive radio frames, starting in the frame where n_f mod 4 = 0, and continuing through frames where n_f mod 4 = 1, 2, and 3.

Input Symbols y^(p)(i)

Each set of 240 bits produces 960 QPSK symbols for normal CP. The same PBCH codeword is effectively reused in subframe 0 of the next three frames, providing four total transmissions over 40 ms.

Mapping Sequence

The 960 symbols y^(p)(i) are mapped into resource elements (REs) in subframe 0 according to the following rules:

Resource Element Indexing: Each RE is identified by (k, l), where k is the subcarrier index (frequency) and l is the OFDM symbol index (time).
Order of Mapping: The standard specifies that the symbols must fill slot 1 in subframe 0 first, in ascending order of k, then l. Once subframe 0 in one frame is filled, the process moves to subframe 0 in the next frame (where n_f increments by 1).
Reference Signal Exclusion: Any REs reserved for cell-specific reference signals (RS) on antenna ports 0–3 are skipped. Even if only one antenna port is actually used, the mapping procedure still accounts for up to four ports’ RS positions, excluding them from PBCH usage.

Four Subframes, One Codeword

The identical 240-bit PBCH codeword is transmitted in subframe 0 for four consecutive frames:

Frame where n_f mod 4 = 0
Frame where n_f mod 4 = 1
Frame where n_f mod 4 = 2
Frame where n_f mod 4 = 3

This repetition ensures the UE can reliably decode the PBCH even if it starts listening mid-way through the 40 ms cycle.

Why This Matters

Repetition for Robustness: Multiple transmissions of the same codeword across four frames improve the chances of successful decoding.
Resource Allocation Consistency: Defining a strict mapping order (first by subcarrier k, then by symbol index l) ensures all UEs know exactly where the PBCH resides.
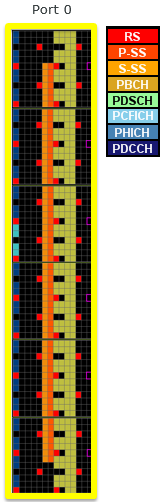
RS Reservation: The requirement to exclude reference signals for antenna ports 0–3 keeps the PBCH mapping consistent regardless of the actual antenna configuration.

PBCH Resource Element Allocation with different Antenna Configuration

Followings are an example of PBCH Resource Element mapping for each of Antenna of 1 Antenna Configuration. (eNB physical cell ID is set to be 0 and System Bandwidth is set to be 20 Mhz).

Followings are an example of PBCH Resource Element mapping for each of Antenna of 4 Antenna Configuration. (eNB physical cell ID is set to be 0 and System Bandwidth is set to be 20 Mhz). At a glance, you would notice a little bit different patters of resource allocation at each antenna. At first, I thought there might be different RE mapping rule for each antenna. However, I don't find any of those differences in 36.211 6.6.4 and then I learned that these different pattern comes from the allocation of null symbol (zero powered symbol) inserted during layer mapping and precoding process.

How to specify Antenna configuration in PBCH

PBCH carry the information about the antenna configuration (the number of Antenna ports being used for a cell). But if you look at the MIB message itself you wouldn't see any information elements about the number of antenna ports. Then how the PBCH can carry the antenna configuration in it ?

It is done by using special CRC mask (the number of bit stream being masked(XORed) over the CRC bits. Number of CRC bits for PBCH is 16 bits, so the length of the CRC mask is 16 bit as well. Following tables shows the types of CRC mask representing each of the antenna configurations.

< 36.212 Table 5.3.1.1-1 : CRC mask for PBCH >

PBCH Eoncoding in srsRAN

If you are interested in this process at the source code level of the protocol stack, I would suggest you to look into the openSource srsRAN. Following APIs can be good places for you to start. This list is from the master-branch of the code that was downloaded on Oct 8,2021

srsran_crc_attach() -> \lib\src\phy\fec\crc.c
srsran_crc_set_mask() -> \lib\src\phy\phch\pbch.c
srsran_convcoder_encode() -> \lib\src\phy\fec\convolutional\convcoder.c
srsran_rm_conv_tx() -> \lib\src\phy\fec\turbo\rm_conv.c
srsran_scrambling_b_offset() -> \lib\src\phy\scrambling\scrambling.c
srsran_mod_modulate() -> \lib\src\phy\modem\mod.c
srsran_layermap_diversity() -> \lib\src\phy\mimo\layermap.c
srsran_precoding_diversity() -> \lib\src\phy\mimo\precoding.c
srsran_pbch_put() -> \lib\src\phy\phch\pbch.c
srsran_pbch_encode() -> \lib\src\phy\phch\pbch.c
srsran_pbch_mib_pack() -> \lib\src\phy\phch\pbch.c

PBCH Decoding in srsRAN

prb_cp_ref() -> \lib\src\phy\phch\prb_dl.c
prb_cp() -> \lib\src\phy\phch\prb_dl.c
srsran_pbch_crc_check() -> \lib\src\phy\phch\pbch.c
srsran_rm_conv_rx() -> \lib\src\phy\fec\turbo\rm_conv.c
srsran_vec_sc_prod_fff() -> \lib\src\phy\utils\vector.c
srsran_viterbi_decode_f() -> \src\phy\fec\convolutional\viterbi.c
decode_frame() -> \lib\src\phy\phch\pbch.c
srsran_pbch_cp() -> \lib\src\phy\phch\pbch.c
srsran_pbch_get() -> \lib\src\phy\phch\pbch.c
srsran_pbch_decode() -> \lib\src\phy\phch\pbch.c
srsran_bit_pack() -> \lib\src\phy\utils\bit.c
srsran_pbch_mib_unpack() -> \lib\src\phy\phch\pbch.c